Contents
clc %clear all close all
System ID
Here I take a bandwidth limited white-noise input, excite a system with it, use arx to build a model of the input/output.
%load strain Ts = 1/1000; % Time-step na = 3; %order denominator model nb = 3; %order numerator model nc = 2; %order numerator noise model (BJ and ARMAX) nd = 2; %order denominator noise model (BJ) output1 = output(8100:8.1*10^4,:); U = output1(:,3); U1 = output1(:,2); Y = output1(:,1); N = length(U); % U = U(8100:(8.2*10^4)); % U1 = U1(8100:(8.2*10^4)); % Y = Y(8100:(8.2*10^4)); % Remove nans if they exist. unan=isnan(U); ynan=isnan(Y); for i=1:length(U) if (unan(i)) U(i) = U(i-1); end if (ynan(i)) Y(i) = Y(i-1); end end unan=isnan(U); ynan=isnan(Y); figure; plot([unan ynan]); % Linearizing data, if needed. K = 0; V = (U -0*K*(U.^3).*(Y)); Y = (2*3.14/2048)*Y; plot([V,Y])
Estimate models using various system ID methods.
highorder = 100;
data=iddata(Y,U1,Ts);
data1=iddata(Y,U,Ts);
data = [data, data1];
data = data(:,1,:) %keep only one of the outputs MISO
nk = delayest(data1);
modelARX = arx(data, [highorder [highorder highorder] [nk nk]]);
modelARX3 = arx(data, [3 [3 3] [nk nk]]);
modelARMAX = armax(data,[na [nb nb] nc [nk nk]]);
modelOE = oe(data, [[nb nb] [na na] [nk nk]]);
modelBJ = bj(data, [[nb nb] nc nd [na na] [nk nk]]);
Time domain data set with 72901 samples.
Sampling interval: 0.001
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
u2
Convert to statespace and returns a decomposition of the model into the observable and unobservable subspaces.
a = idss(modelARX); [A,B,C,T,k] = obsvf(a.A,a.B,a.C); sys = ss(A,B,C,a.D,modelARX.Ts); a = idss(modelARX3); [A,B,C,T,k] = obsvf(a.A,a.B,a.C); sysARX3 = ss(A,B,C,a.D,modelARX3.Ts); a = idss(modelARMAX); [A,B,C,T,k] = obsvf(a.A,a.B,a.C); sysARMAX = ss(A,B,C,a.D,modelARMAX.Ts); a = idss(modelOE); [A,B,C,T,k] = obsvf(a.A,a.B,a.C); sysOE = ss(A,B,C,a.D,modelOE.Ts); a = idss(modelBJ); [A,B,C,T,k] = obsvf(a.A,a.B,a.C); sysBJ = ss(A,B,C,a.D,modelBJ.Ts);
Order Reduction
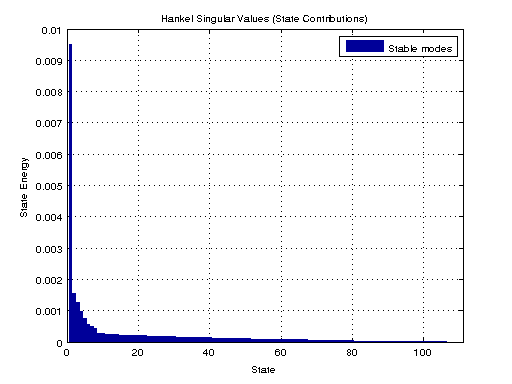
Computes the Hankel singular values hsv of the dynamic system sys. In state coordinates that equalize the input-to-state and state-to-output energy transfers, the Hankel singular values measure the contribution of each state to the input/output behavior. Hankel singular values are to model order what singular values are to matrix rank.
We then use balred to reduce the model order through use of a balanced realization.
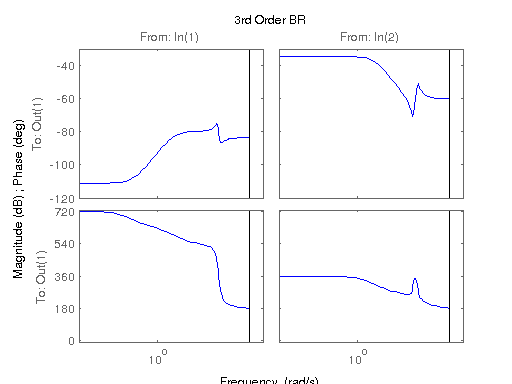
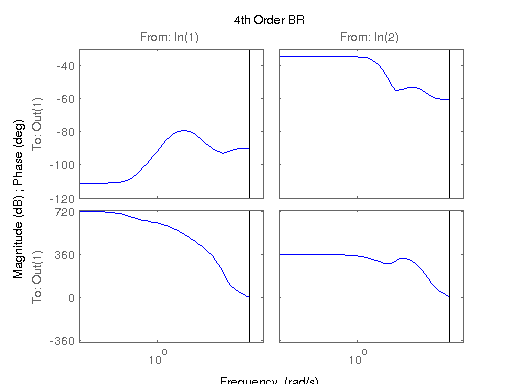
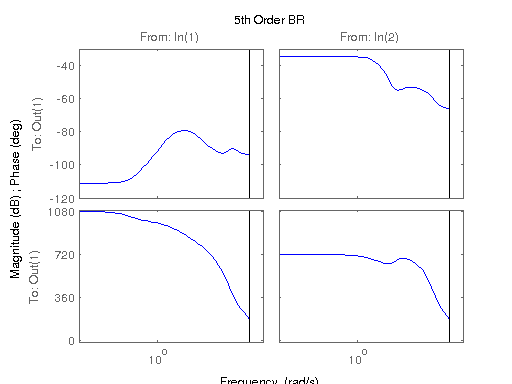
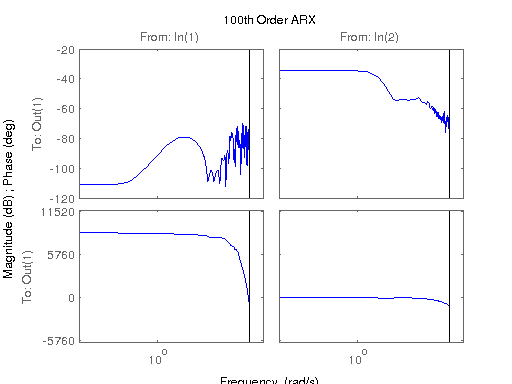
figure; hsvd(sys); % Check out what orders contain the most amount of energy. sys3 = balred(sys, 3) sys4 = balred(sys, 4) sys5 = balred(sys, 5) figure; bode(sys3); title('3rd Order BR'); figure; bode(sys4); title('4th Order BR'); figure; bode(sys5); title('5th Order BR'); figure; bode(sys); title('100th Order ARX'); figure; bode(sysARX3); title('3rd Oder ARX'); figure; bode(sysOE); title('OE Model'); figure; bode(sysBJ); title('BJ Model'); figure; bode(sysARMAX); title('ARMAX Model');
a =
x1 x2 x3
x1 0.953 0.2052 0.01946
x2 -0.09065 1.098 0.2412
x3 0.06411 -0.1237 0.8559
b =
u1 u2
x1 -1.856e-06 -0.002165
x2 0.0001254 0.0001829
x3 -7.085e-05 0.0002413
c =
x1 x2 x3
y1 -0.1186 -0.01792 -0.1334
d =
u1 u2
y1 -6.173e-05 -0.0008695
Sampling time (seconds): 0.001
Discrete-time state-space model.
a =
x1 x2 x3 x4
x1 0.7566 -0.1398 0.5856 -0.2578
x2 0.2515 0.9966 -0.1714 0.1034
x3 0.0448 0.06568 0.7407 0.1338
x4 -0.007778 -0.01769 0.06589 0.9607
b =
u1 u2
x1 -0.0001264 -0.005856
x2 4.28e-05 0.0006873
x3 6.846e-05 0.002724
x4 -2.002e-05 -0.00096
c =
x1 x2 x3 x4
y1 0.04525 -0.1192 -0.1168 0.01011
d =
u1 u2
y1 1.887e-05 0.0004616
Sampling time (seconds): 0.001
Discrete-time state-space model.
a =
x1 x2 x3 x4 x5
x1 0.6903 -0.5091 -0.3041 0.4811 -0.1035
x2 0.1544 0.7294 -0.1825 0.8653 -0.0009059
x3 0.2542 0.1104 1.092 -0.2477 0.06413
x4 -0.05073 0.06509 0.07993 0.4394 -0.03276
x5 0.02531 -0.1257 -0.0902 0.3841 0.9944
b =
u1 u2
x1 -7.601e-05 0.0007801
x2 -0.0001636 -0.004855
x3 3.768e-05 0.001123
x4 0.0001206 0.003997
x5 -7.311e-05 -0.001823
c =
x1 x2 x3 x4 x5
y1 -0.04945 -0.03785 0.1087 0.0277 0.0246
d =
u1 u2
y1 -4.194e-06 -0.0001146
Sampling time (seconds): 0.001
Discrete-time state-space model.
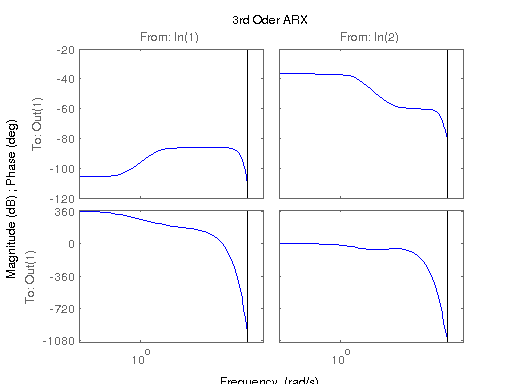
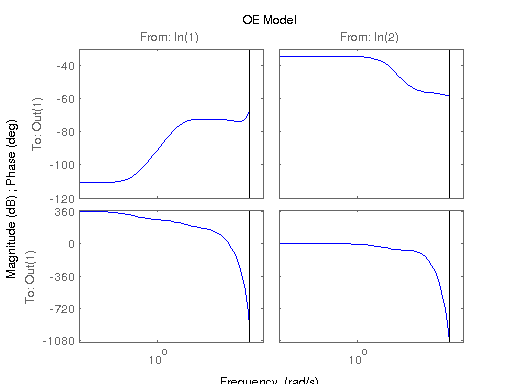
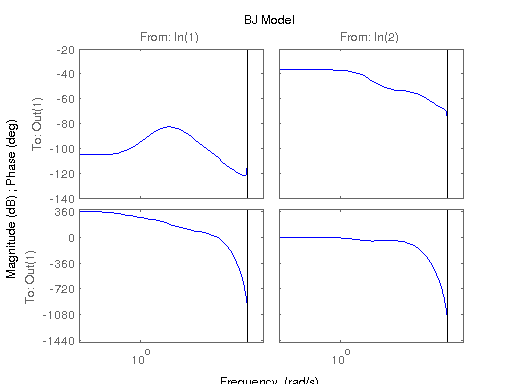
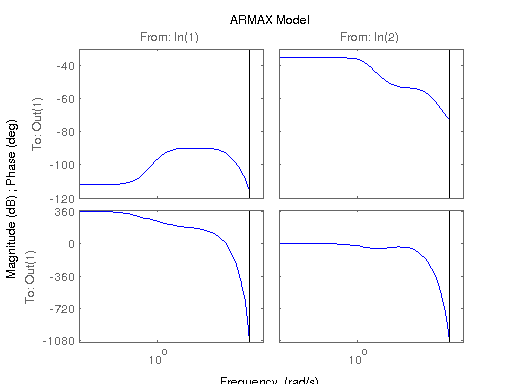
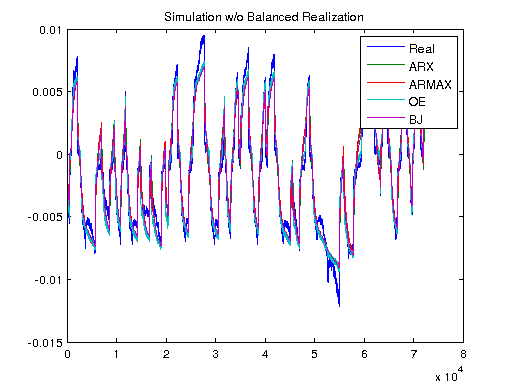
Simulation Of Models To Real Data
Using lsim to look at the differences between the actual data, and what our models will predict the output to be.
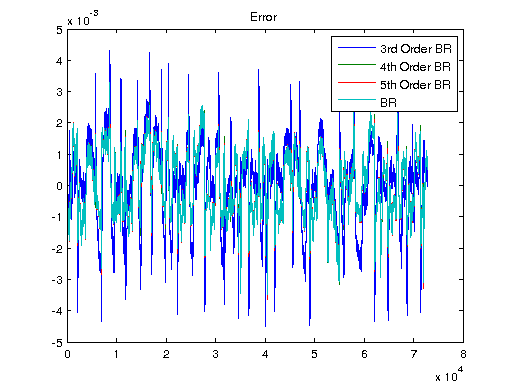
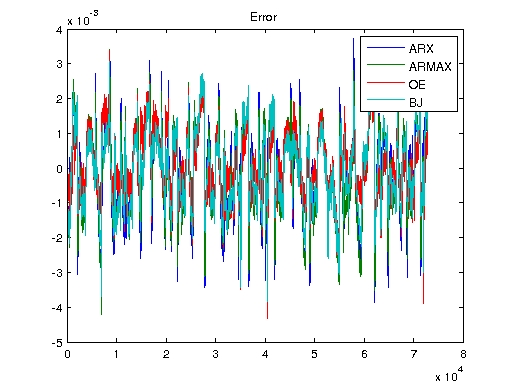
Ts = 1/1000; V = [U1, U]; T = Ts*(0:length(V)-1); y3 = lsim(sys3, V); y4 = lsim(sys4, V); y5 = lsim(sys5, V); ysys = lsim(sys, V); yARX3 = lsim(sysARX3, V); yARMAX = lsim(sysARMAX, V); yOE = lsim(sysOE, V); yBJ = lsim(sysBJ, V); figure plot([Y y3 y4 y5 ysys]) legend('Real','3rd Order BR','4th Order BR','5th Order BR', 'BR'); title('Simulation of Order-Reduction and Balanced Realization'); plot([Y yARX3 yARMAX yOE yBJ]) legend('Real','ARX','ARMAX','OE', 'BJ'); title('Simulation w/o Balanced Realization'); figure plot([Y-y3 Y-y4 Y-y5 Y-ysys]) title('Error'); legend('3rd Order BR','4th Order BR','5th Order BR', 'BR'); figure plot([Y-yARX3 Y-yARMAX Y-yOE Y-yBJ]) title('Error'); legend('ARX','ARMAX','OE', 'BJ');
Non-Linear Model
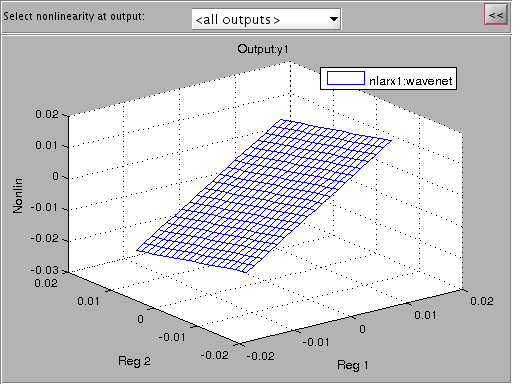
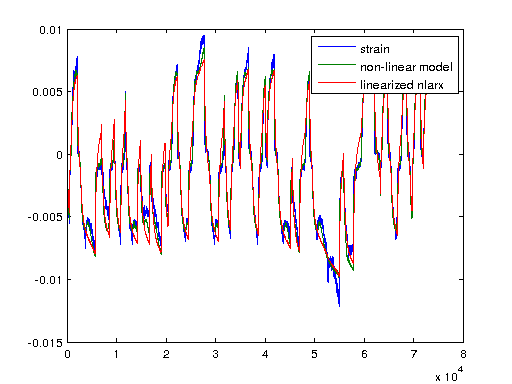
I'm plotting a non-linear ARX model of the system here with 5 regressors and a wavelet network with 57 units which was modeled to the same iddata object. First we'll look at the non-linearity of the wavenet and then simulate the output strain with both the non-linear model and a linearized verion of the nonlinear autoregressive approximation using linapp. Linapp does /not/ use a tangent linearization approach and should work better for larger ranges of input 'u'.
figure; plot(nlarx1); figure; a = linapp(nlarx1,V); a = idss(a); a = ss(a.A, a.B, a.C, a.D, 1/1000); plot([Y sim(nlarx1, V) lsim(a, V)]); legend('strain', 'non-linear model', 'linearized nlarx');